AOJ - CLOCKSYNC
on Algorithm
출처 AOJ
Synchronizing clocks
문제
4 x 4 개의 격자 형태로 배치된 16개의 시계가 있다. 이 시계들은 모두 12시, 3시, 6시, 혹은 9시를 가리키고 있다. 이 시계들이 모두 12시를 가리키도록 바꾸고 싶다.
시계의 시간을 조작하는 유일한 방법은 모두 10개 있는 스위치들을 조작하는 것으로, 각 스위치들은 모두 적게는 3개에서 많게는 5개의 시계에 연결되어 있다. 한 스위치를 누를 때마다, 해당 스위치와 연결된 시계들의 시간은 3시간씩 앞으로 움직인다.(12시→3시, 3시→6시, 6시→9시, 9시→12시) 스위치들과 그들이 연결된 시계들의 목록은 다음과 같다.
| 스위치 | 연결된 시계 |
|---|---|
| 0 | 0, 1, 2 |
| 1 | 3, 7, 9, 11 |
| 2 | 4, 10, 14, 15 |
| 3 | 0, 4, 5, 6, 7 |
| 4 | 6, 7, 8, 10, 12 |
| 5 | 0, 2, 14, 15 |
| 6 | 3, 14, 15 |
| 7 | 4, 5, 7, 14, 15 |
| 8 | 1, 2, 3, 4, 5 |
| 9 | 3, 4, 5, 9, 13 |
시계들은 맨 윗줄부터, 왼쪽에서 오른쪽으로 순서대로 번호가 매겨졌다고 가정하자. 시계들이 현재 가리키는 시간들이 주어졌을 때, 모든 시계를 12시로 돌리기 위해 최소한 눌러야 할 스위치의 수를 계산하는 프로그램을 작성하시오.
입력
첫 줄에 테스트 케이스의 개수 C (<= 30) 가 주어진다. 각 테스트 케이스는 한 줄에 16개의 정수로 주어지며, 각 정수는 0번부터 15번까지 각 시계가 가리키고 있는 시간을 12, 3, 6, 9 중 하나로 표현한다.
출력
각 테스트 케이스당 한 줄을 출력한다. 시계들을 모두 12시로 돌려놓기 위해 눌러야 할 스위치의 최소 수를 출력한다. 만약 이것이 불가능할 경우 -1 을 출력한다.
예제
입력
2
12 6 6 6 6 6 12 12 12 12 12 12 12 12 12 12
12 9 3 12 6 6 9 3 12 9 12 9 12 12 6 6
출력
2
9
범위체크
최대 누르는 횟수 = 3^{10} < INT
풀이
한번 누를때마다 (clock+3)%12로 변화
→ 4번이상 누르는건 의미 없음(다시 반복됨)
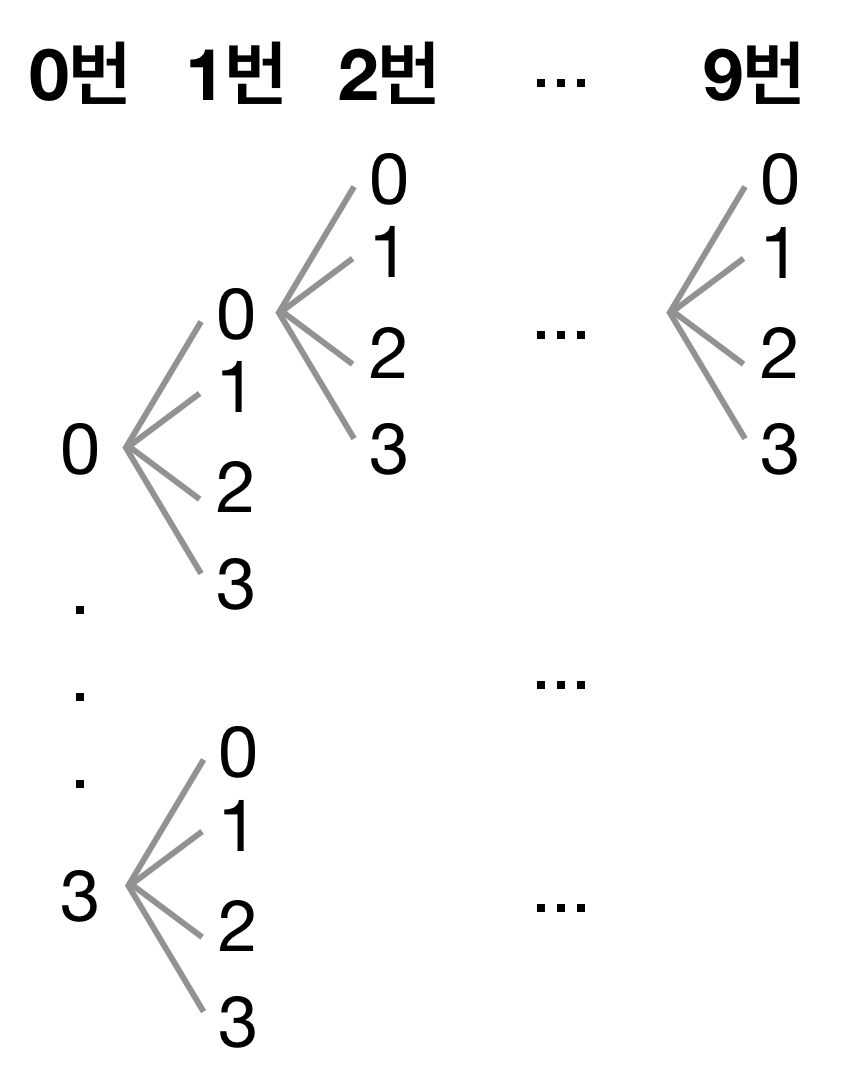 그림과 같이 동작하므로
그림과 같이 동작하므로
{i번 스위치를 0~4번 누르고 각각 경우에 다음 스위치 누르기}
시계가 모두 0(==12)이거나 스위치가 10이 될때까지 반복
코드
#include<cstdio>
#include<vector>
#define UPPER 987654321
using namespace std;
vector<int> S[10] = { {0,1,2},{3,7,9,11},{4, 10, 14, 15},{0, 4, 5, 6, 7},{6, 7, 8, 10, 12},
{0, 2, 14, 15},{3, 14, 15},{4, 5, 7, 14, 15},{1, 2, 3, 4, 5},{3, 4, 5, 9, 13} };
int MIN;
void pushSwitch(int* CLOCK, int btn, int cnt){
int flag = 1;
for(int i=0; i<16; i++){
if(CLOCK[i] != 0){
flag = 0;
break;
}
}
if(flag){
if(MIN > cnt)
MIN = cnt;
}
else{
for(int i=0; btn<10 && i<4; i++){
for(int j=0; j<S[btn].size(); j++)
CLOCK[S[btn][j]] = (CLOCK[S[btn][j]] + 3) %12;
pushSwitch(CLOCK,btn+1, cnt+(i+1)%4);
}
}
}
int main(){
int testcase;
scanf("%d",&testcase);
while(testcase--){
int CLOCK[16];
for(int i=0; i<16; i++){
scanf("%d",&CLOCK[i]);
CLOCK[i] = CLOCK[i]%12;
}
MIN = UPPER;
pushSwitch(CLOCK,0,0);
if(MIN==UPPER)
MIN = -1;
printf("%d\n",MIN);
}
}
복잡도
O(4^{10})
10개의 스위치를 4가지 방법으로 동작시키는 경우의 수 이므로