BOJ 1707 - 이분 그래프

10 Mar 2017 on Algorithm

출처 BOJ

이분 그래프

문제

그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 (Bipartite Graph) 라 부른다.

그래프가 입력으로 주어졌을 때, 이 그래프가 이분 그래프인지 아닌지 판별하는 프로그램을 작성하시오.

입력

입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K(2≤K≤5)가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V(1≤V≤20,000)와 간선의 개수 E(1≤E≤200,000)가 빈 칸을 사이에 두고 순서대로 주어진다. 각 정점에는 1부터 V까지 차례로 번호가 붙어 있다. 이어서 둘째 줄부터 E개의 줄에 걸쳐 간선에 대한 정보가 주어지는데, 각 줄에 인접한 두 정점의 번호가 빈 칸을 사이에 두고 주어진다.

출력

K개의 줄에 걸쳐 입력으로 주어진 그래프가 이분 그래프이면 YES, 아니면 NO를 순서대로 출력한다.

예제

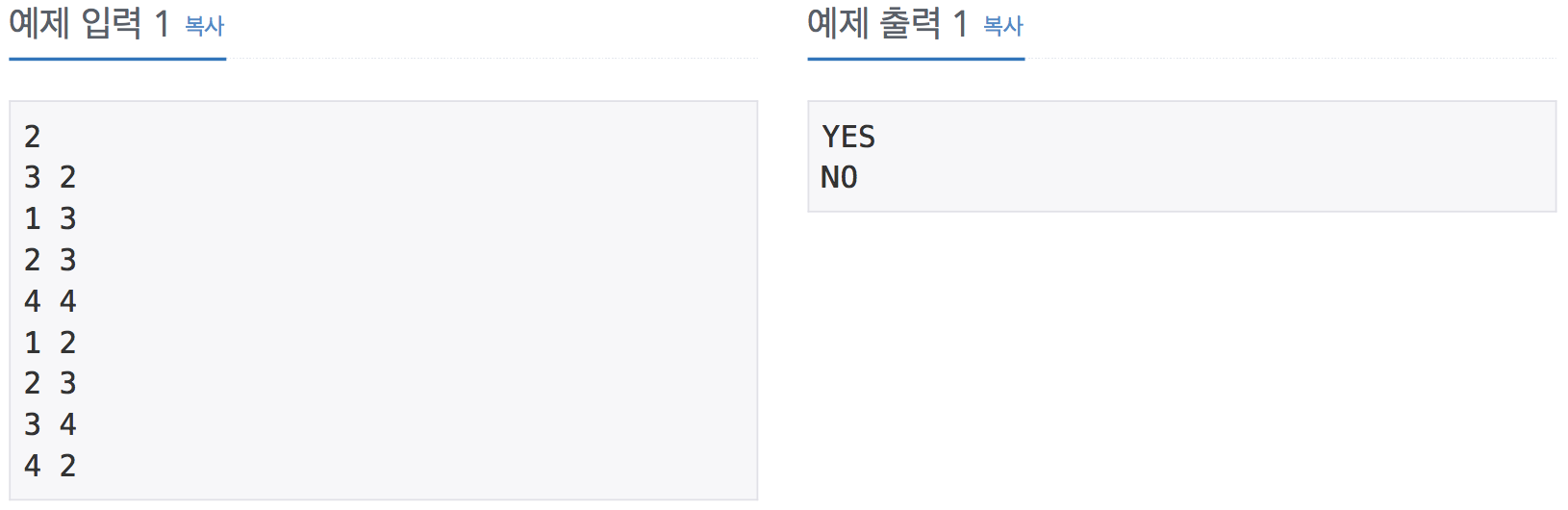
범위체크

연산 따로 없음

풀이

첫 노드부터 연결된 애는 다른 그룹으로 분류 → BFS로 반복해서 분류
만약 그룹이 있는데 다른 그룹으로 변경되려고하는 경우(= 같은 그룹의 노드와 연결된 경우) → FALSE
아래 그림과 같이 1,3이 같은 그룹에 속하면서 연결된 경우는 Bipartite 그래프가 될 수 없음

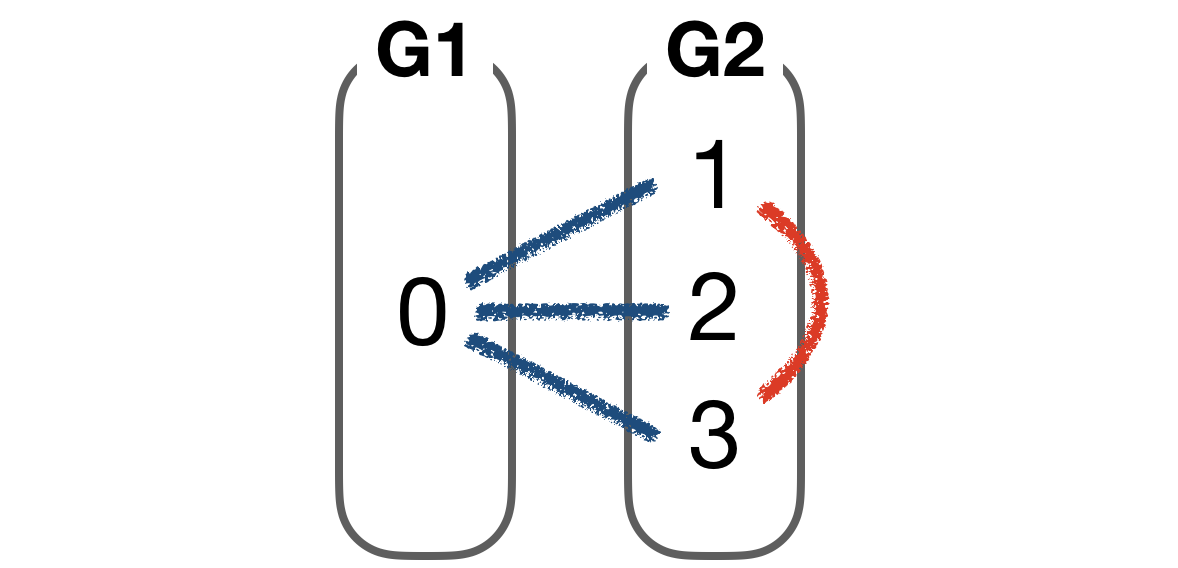
주의할 것!!
노드들이 모두 연결된 그래프가 아닐 수 있음!(연결요소 1이상)

코드

code

#include<cstdio>
#include<queue>
#include<vector>
#define MAX 20001

using namespace std;

int V;
vector<int> G[MAX];
queue<pair<int,int> > Q;
int check[MAX];
int flag;

void bfs(){
	while(!Q.empty()){
		int now = Q.front().first;
		int before = Q.front().second;
		Q.pop();
		for(auto i=0; i<G[now].size(); i++){
			int next = G[now][i];
			if(next != before){
				int temp = (check[now]+1)%2;
				if(check[next] == -1){
					check[next] = temp;
					Q.push(make_pair(next,now));
				}
				else{
					if(check[next] != temp)
						flag = 1;
				}
			}
		}
	}
}

int main(){
	int testcase;
	scanf("%d",&testcase);
	while(testcase--){
		int E;
		scanf("%d%d",&V,&E);
		flag = 0;
		fill_n(check,V,-1);
		while(E--){
			int x,y;
			scanf("%d%d",&x,&y);
			G[x-1].push_back(y-1);
			G[y-1].push_back(x-1);
		}
	
		for(int i=0; i<V; i++){
			if(check[i] == -1){
				check[i] = 0;
				Q.push(make_pair(i,-1));
				bfs();
			}
		}
	
		if(flag)
		printf("NO\n");	
		else
		printf("YES\n");
	
		for(int i=0; i<V; i++)
			G[i].clear();
	}
}

복잡도

$O(V+E)$
BFS탐색을 사용하여 E개의 엣지를 이동하고 V개의 노드를 방문했기 때문에