출처 BOJ

붕어빵 판매하기

문제

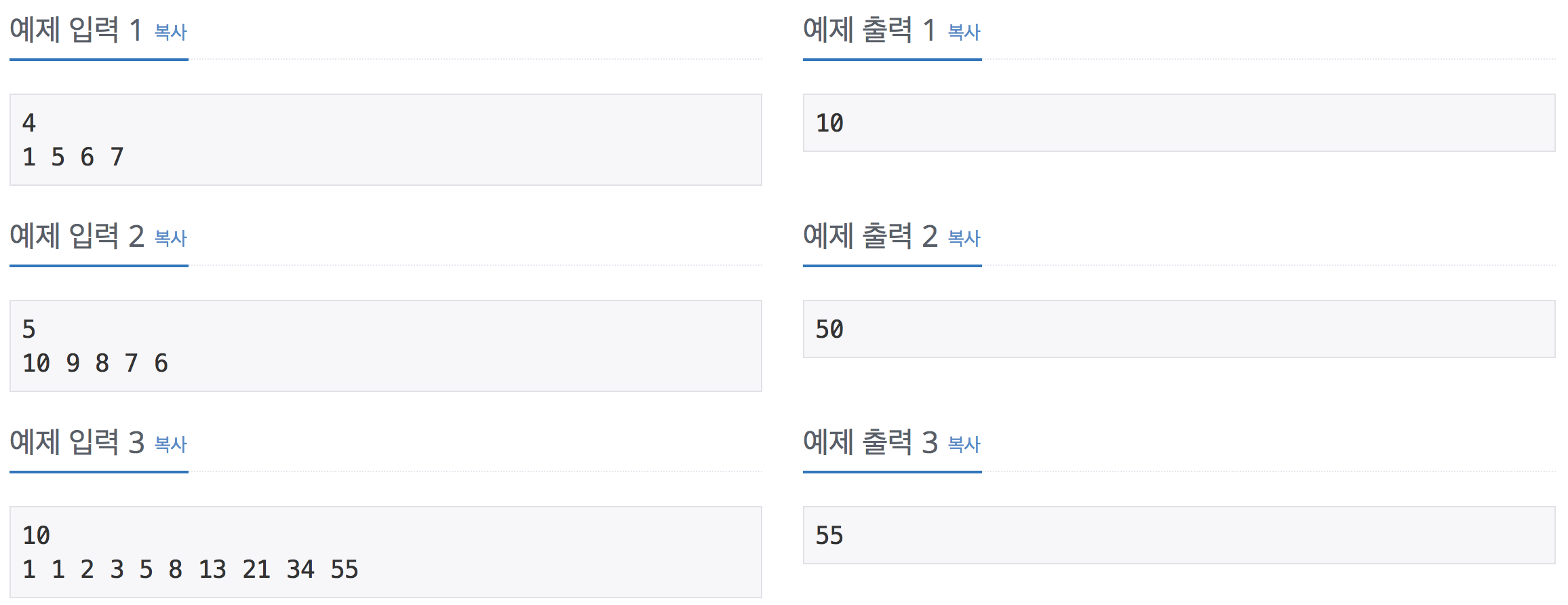
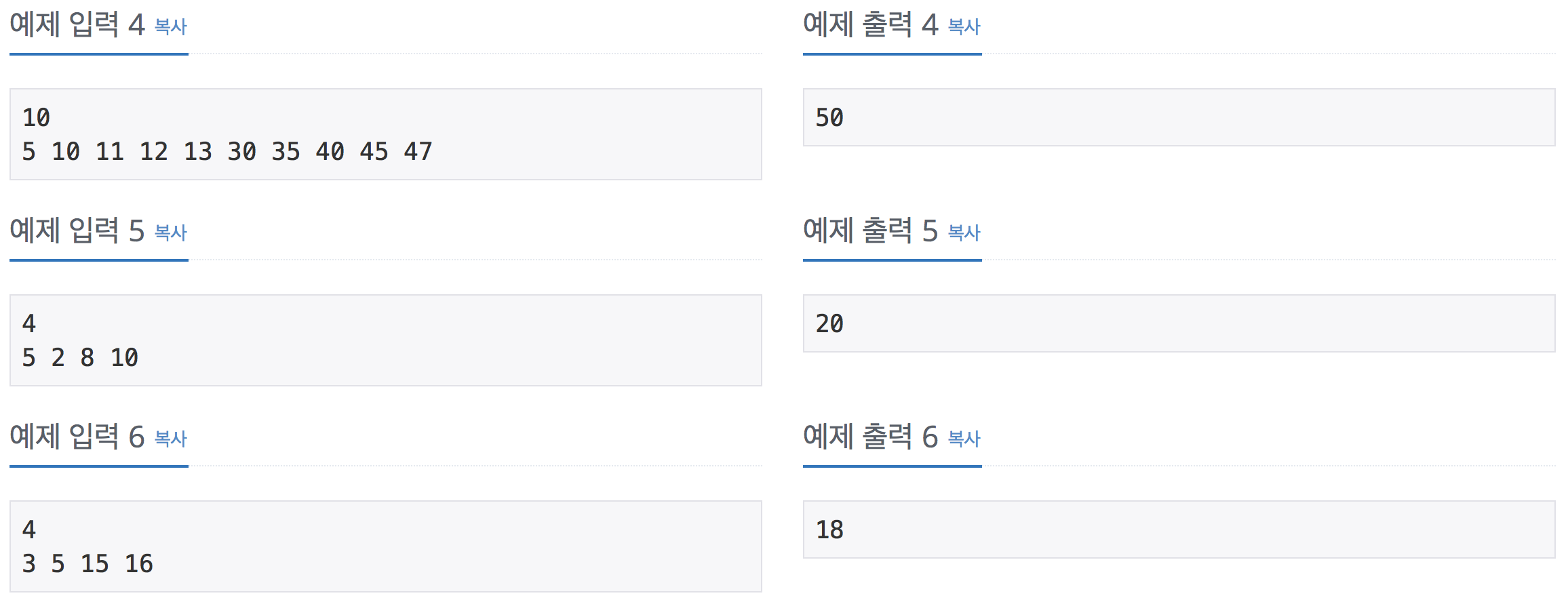
강남역에서 붕어빵 장사를 하고 있는 해빈이는 지금 붕어빵이 N개 남았다.

해빈이는 적절히 붕어빵 세트 메뉴를 구성해서 붕어빵을 팔아서 얻을 수 있는 수익을 최대로 만드려고 한다. 붕어빵 세트 메뉴는 붕어빵을 묶어서 파는 것을 의미하고, 세트 메뉴의 가격은 이미 정해져 있다.

붕어빵 i개로 이루어진 세트 메뉴의 가격은 Pi 원이다.

붕어빵이 4개 남아 있고, 1개 팔 때의 가격이 1, 2개는 5, 3개는 6, 4개는 7인 경우에 해빈이가 얻을 수 있는 최대 수익은 10원이다. 2개, 2개로 붕어빵을 팔면 되기 때문이다.

1개 팔 때의 가격이 5, 2개는 2, 3개는 8, 4개는 10 인 경우에는 20이 된다. 1개, 1개, 1개, 1개로 붕어빵을 팔면 되기 때문이다.

마지막으로, 1개 팔 때의 가격이 3, 2개는 5, 3개는 15, 4개는 16인 경우에는 정답은 18이다. 붕어빵을 3개, 1개로 팔면 되기 때문이다.

세트 메뉴의 가격이 주어졌을 때, 해빈이가 얻을 수 있는 최대 수익을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 해빈이가 가지고 있는 붕어빵의 개수 N이 주어진다. (1 ≤ N ≤ 1,000)
둘째 줄에는 Pi가 P1부터 PN까지 순서대로 주어진다. (1 ≤ Pi ≤ 10,000)

출력

해빈이가 얻을 수 있는 최대 수익을 출력한다.

예제

범위체크

최대가격($10^{4}$) x 최대개수($10^{3}$) $= 10^{7} \le INT$

풀이

작은 문제로 분리가능 & 각 개수일때 최대값 구하기로 결과 구할 수 있음 → DP! 각 단계 최대값 $M[N] = max(M[N-k]+M[k])$
ex) 4개일 때 최대값
$M[4] = \left(\begin{array}{c} M[4]+M[0]\\ M[3]+M[1]\\ M[2]+M[2] \end{array}\right)$ 값들 중 최대값

코드

code

#include<cstdio>
#include<iostream>
#define BOUND 1001
using namespace std;

int N;
int P[BOUND];
int M[BOUND];

void sell(){
	for(int i=1; i<N; i++){
		int before = 0;
		M[i] = P[i];
		for(int j = i; j*2 >= i; j--)
			before = max(M[i-j]+M[j],before);
		M[i] = before;
	}
	printf("%d\n",M[N-1]);
}

int main(){
	scanf("%d",&N);
	N = N+1;
	M[0] = P[0] = 0; 
	for(int i=1; i<N; i++){
		scanf("%d",&P[i]);
	}

	sell();
}

복잡도

$O(N{N \over 2})$
N개까지 확인 x 각 단계에서 max값을 구하기 위한 loop횟수