BOJ 2146 - 다리만들기
on Algorithm
출처 BOJ
다리만들기
문제
여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은, 섬들을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다는 생각을 하게 되었다. 그래서 그는, 생색내는 식으로 한 섬과 다른 섬을 잇는 다리 하나만을 만들기로 하였고, 그 또한 다리를 가장 짧게 하여 돈을 아끼려 하였다.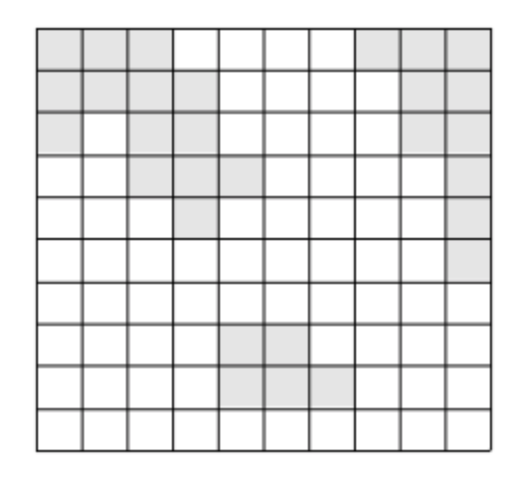 
위의 그림에서 색이 있는 부분이 육지이고, 색이 없는 부분이 바다이다. 이 바다에 가장 짧은 다리를 놓아 두 대륙을 연결하고자 한다. 가장 짧은 다리란, 다리가 격자에서 차지하는 칸의 수가 가장 작은 다리를 말한다. 다음 그림에서 두 대륙을 연결하는 다리를 볼 수 있다. 
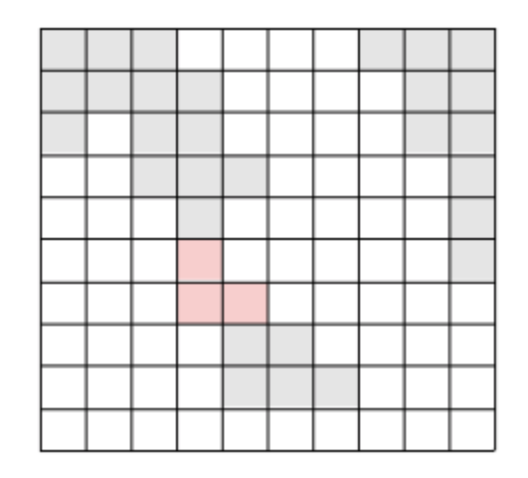물론 위의 방법 외에도 다리를 놓는 방법이 여러 가지 있으나, 위의 경우가 놓는 다리의 길이가 3으로 가장 짧다(물론 길이가 3인 다른 다리를 놓을 수 있는 방법도 몇 가지 있다).
지도가 주어질 때, 가장 짧은 다리 하나를 놓아 두 대륙을 연결하는 방법을 찾으시오.
이 나라는 N×N크기의 이차원 평면상에 존재한다. 이 나라는 여러 섬으로 이루어져 있으며, 섬이란 동서남북으로 육지가 붙어있는 덩어리를 말한다. 다음은 세 개의 섬으로 이루어진 나라의 지도이다.
입력
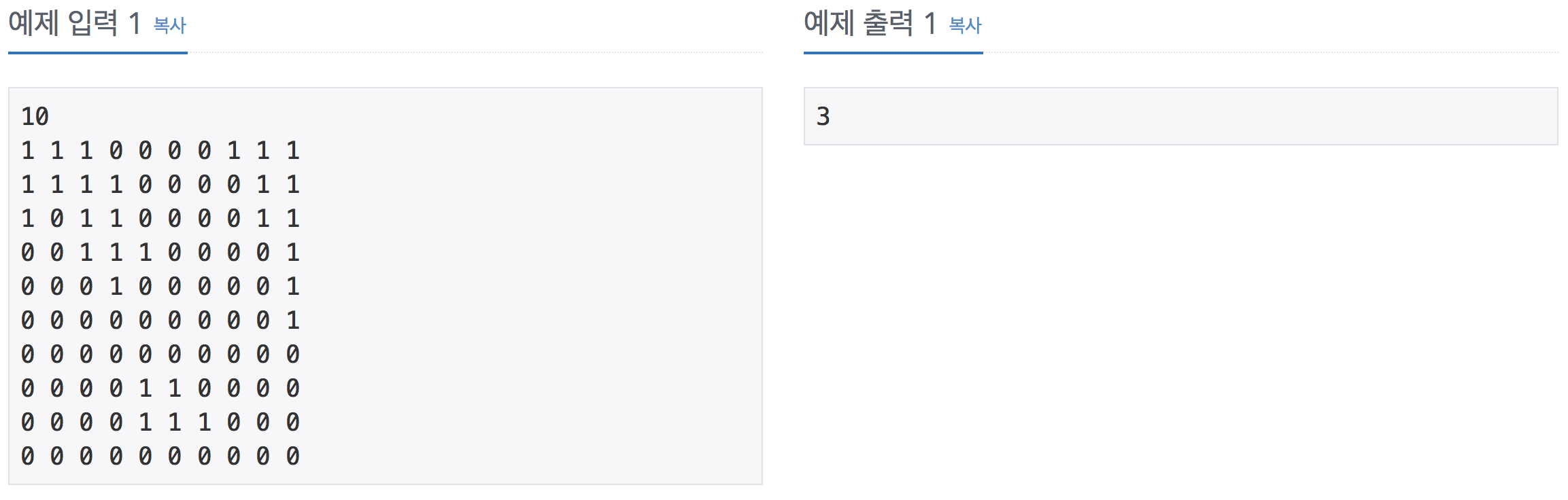
첫 줄에는 지도의 크기 N(100이하의 자연수)가 주어진다. 그 다음 N줄에는 N개의 숫자가 빈칸을 사이에 두고 주어지며, 0은 바다, 1은 육지를 나타낸다.
출력
첫째 줄에 구한 0의 개수를 출력한다.
예제
범위체크
총 격자수 100x100 \le INT
풀이
- 섬을 구분하기
bfs나 dfs로 각 위치 구분해놓기 - 각각 섬에서 확산하면서 영토 넓히기
& 다른지도에는 몇번만에 해당위치를 갔는지 기록 - 인접한 곳과 영토가 다른 곳 찾기, 그 위치들의 cnt값 합 중 최소값찾기
코드
#include<cstdio>
#include<queue>
#define BOUND 101
#define MIN 987654321
using namespace std;
int M[BOUND][BOUND];
int C[BOUND][BOUND];
int N;
queue<pair<int,int> > Q;
queue<pair<int,int> > sQ;
int dir[4][2] = { {0,1},{1,0},{0,-1},{-1,0} };
void seperateL(){
while(!Q.empty()){
int x = Q.front().first;
int y = Q.front().second;
sQ.push(make_pair(x,y));
Q.pop();
for(int i=0; i<4; i++){
int tx = x+dir[i][0];
int ty = y+dir[i][1];
if(0<=tx && tx <N && 0<=ty && ty <N && M[tx][ty]==0){
M[tx][ty] = M[x][y];
Q.push(make_pair(tx,ty));
}
}
}
}
void spread(){
while(!sQ.empty()){
int x = sQ.front().first;
int y = sQ.front().second;
sQ.pop();
for(int i=0; i<4; i++){
int tx = x+dir[i][0];
int ty = y+dir[i][1];
if(0<=tx && tx <N && 0<=ty && ty <N && M[tx][ty]==-1){
M[tx][ty] = M[x][y];
C[tx][ty] = C[x][y] +1;
sQ.push(make_pair(tx,ty));
}
}
}
}
int main(){
scanf("%d",&N);
for(int i=0; i<N; i++){
for(int j=0; j<N; j++){
scanf("%d",&M[i][j]);
M[i][j] = -1+M[i][j];
C[i][j] = 0;
}
}
int cnt = 1;
for(int i=0; i<N; i++){
for(int j=0; j<N; j++){
if(M[i][j] == 0){
M[i][j] = cnt;
Q.push(make_pair(i,j));
seperateL();
cnt++;
}
}
}
spread();
int min = MIN;
for(int i=0; i<N; i++){
for(int j=0; j<N; j++){
for(int t=0; t<4; t++){
int tx = i+dir[t][0];
int ty = j+dir[t][1];
if(0<=tx && tx <N && 0<=ty && ty <N && M[tx][ty]!=M[i][j]){
int val = C[i][j] + C[tx][ty];
if(min > val)
min = val;
}
}
}
}
if(min == MIN)
min = 0;
printf("%d\n",min);
}
복잡도
O(N^2)
모든 칸 확인하는 것이 가장 오래 걸리는