Event Threading within News Topics 정리

Connecting the dots의 User study에서 competitor로 나온 방법
정리 순서

• Event Threading in Connecting the dots
  • Brief definiton of Event Threading
  • How Event Threading Used in CTD
• Details of Event Threading
  • Notation
  • The difference between Event Threading and TDT
  • Problem Definition
  • Modeling(Clustering stories & Constructing Dependencies)

Event Threading in Connecting the dots

Brief Definition of Event Threading

Event Threading은 news event에서 sub-cluster를 찾고 dependency로 구조화하여 graph를 만드는 방법이다. 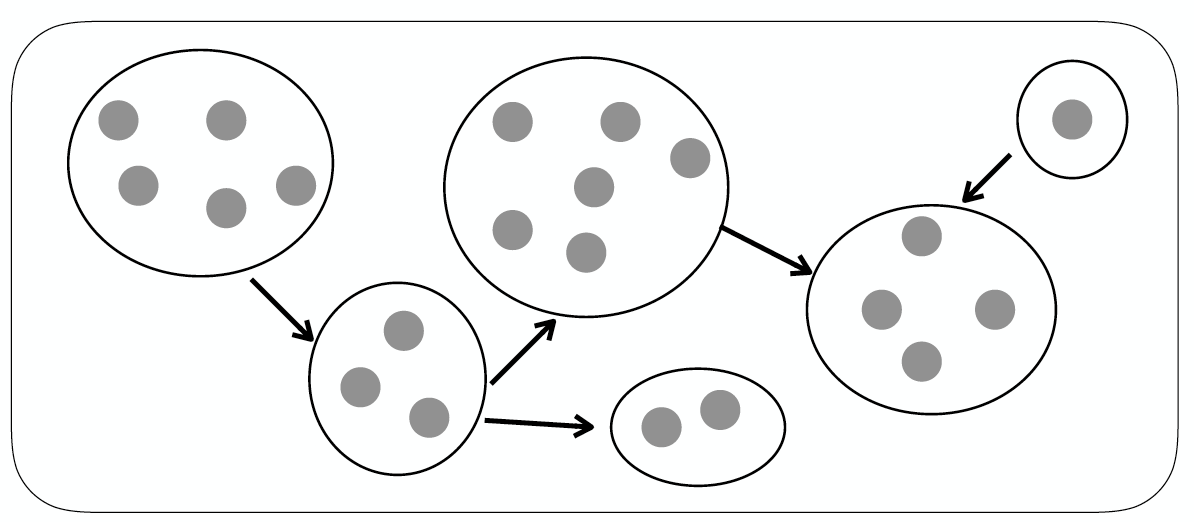위의 그림에서처럼 news event가 cluster로 묶이고 각각의 상관관계에 따라 dependency로 연결되어 그래프를 구성하는 형태이다.

How Event Threading used in CTD

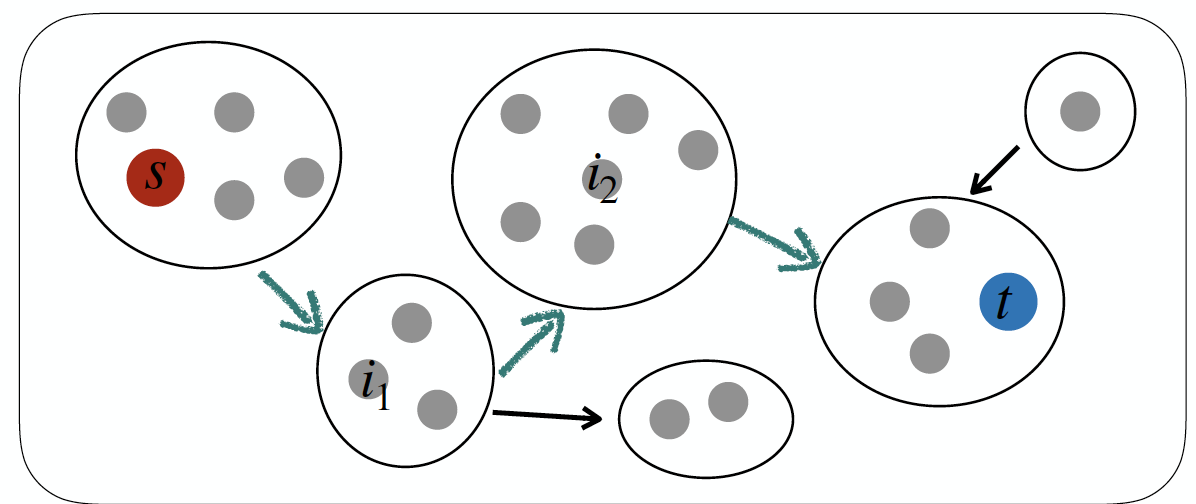CTD와 비교하기 위해 news article들의 연결을 찾는 방법은 다음과 같다.

1. s를 포함하는 cluster에서 t를 포함하는 cluster까지의 경로를 찾는다.
2. 경로에 있는 각 cluster를 대표하는 article을 찾는다.
3. 만약 chain이 너무 길다면, K equally-spaced하게 article을 선택한다.

Details of Event Threading

Notation

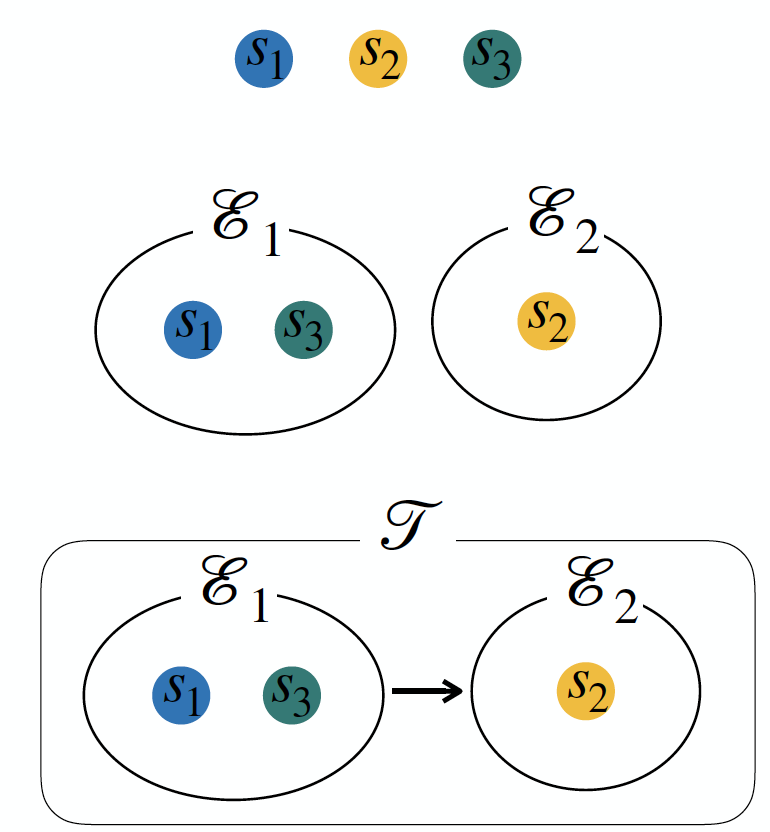
• Story : the smallest atomic unit in the hierarchy (Topic > Event > Story)
• Event : a set of stories, a set of non-overlapping clusters ($\because$ assumption of atomicity of a story)
• Topic : a series of related events / clusters of stories( = events) & edges between pairs of these clusters(= dependencies between these events)

The difference between Event Threading and TDT

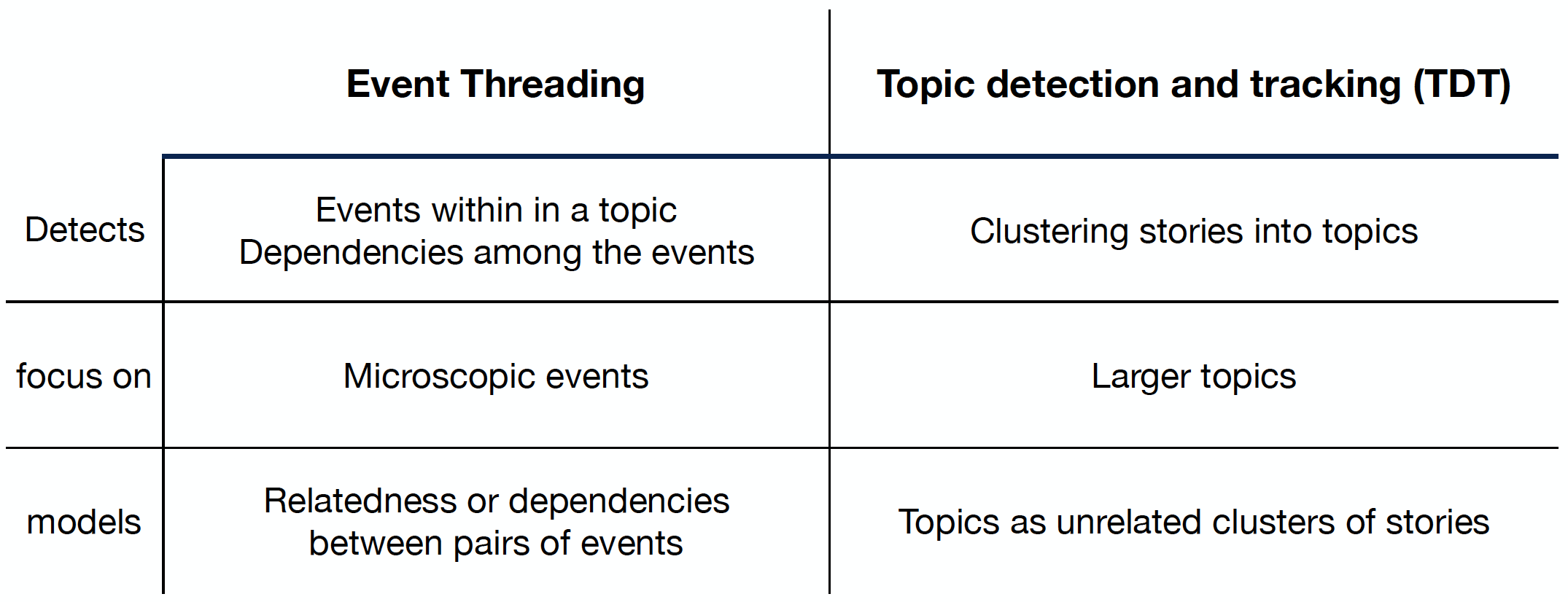
Problem Definition

• Given : a set of $n$ news stories ($S = {s_1,...,s_n}$) on given topic $T$ and their time of publication
  → define a set of events $\mathcal{E} = \{\mathcal{E}_1, ..., \mathcal{E}_m\}$
  with the following constraints :
  $\forall i \quad \mathcal{E}_i \in 2^{S}$
  $\forall i,j \quad s.t.\ i \neq j,\ \mathcal{E}_i \cap \mathcal{E}_j = \{\}$
  $\forall s_{i} \quad \exists \quad \mathcal{E}_k \in \mathcal{E}\ s.t.\ s_{i} \in \mathcal{E}_k$

  첫번째 제약조건은 Event i는 story의 부분집합에 속한다는 의미이고 두번째는 Notation에서 언급한것 처럼 Event는 non-overlapping하고 세번째는 모든 story는 한개의 Event에 포함된다는 것이다.

• Find : structure of events and their dependencies in a news topic

Event Modeling(Clustering stories & Constructing Dependencies)

Modeling은 Clustering과 Dependency를 생성하는 것으로 나뉜다.

Clustering stories

• Features which indicate similarity between two stories
  • Inner product of their tf-idf vectors
  • Time stamp (Stories in the same event tend to follow temporal locality)
  • Named-entities such as person and location names
    두 story간의 유사도는 위의 3가지 특징으로 나타낼 수 있고
    → agglomerative clustering algorithm을 통해 특징들을 통합하여 표현한다.

• Agglomerative clustering with time decay (ACDT) Initialize events to singleton events(clusters) event를 singleton으로 표현함으로써 similarity between events = similarity between stories 가 된다.
  $wsum(s_1,s_2) = w_1cos(s_1,s_2)\ +\ w_2Loc(s_1,s_2)\ +\ w_3Per(s_1,s_2)$
  $w_1,w_2,w_3$ : weights on different features. Determine them empirically
  $cos(s_1,s_2)$ : cosine similarity of term vectors
  $Loc(s_1,s_2)$: 1 if there is some location appears in both stories, otherwise 0
  $Per(s_1,s_2)$: similarity defined for person name

• Time decay
  시간의 차이가 커질수록 유사도를 줄어들도록 식을 수정한다.
  $sim(s_1,s_2) = wsum(s_1,s_2)e^{- \alpha \|t_1-t_2\| \over T}$ $\alpha$ : Time decay factor
  $t_1,t_2$ : Time stamps for story 1, story 2
  $T$ : Time difference between two story

• 3 ways to compute the similarity between two events
  • Average link
    $sim(\mathcal{E}_u,\mathcal{E}_v) = {\sum_{s_u \in \mathcal{E}_u} \sum_{s_v \in \mathcal{E}_v} sim(s_u,s_v) \over \|\mathcal{E}_u\|\|\mathcal{E}_v\|}$
  • Complete link
    $sim(\mathcal{E}_u,\mathcal{E}_v) = min_{ {s_u \in \mathcal{E}_u},{s_v \in \mathcal{E}_v} }sim(s_u,s_v)$
  • Single link
    $sim(\mathcal{E}_u,\mathcal{E}_v) = max_{ {s_u \in \mathcal{E}_u},{s_v \in \mathcal{E}_v} }sim(s_u,s_v)$

각 iteration에 most similar event pair를 찾고 merge한다. 이 과정을 maximum similarity가 threshold이하거나 cluster의 수가 주어진 수보다 작을때 까지만 반복한다.

Constructing Dependencies

time-ordering과 word distribution과 같은 surface-feature만 고려한다.

• Define a couple of features that the following models will employ
  • Event-time-ordering function
    $t_e: \quad \mathcal{E} \rightarrow \{1, ... ,m\}\ s.t.$ $\forall \mathcal{E}_u,\mathcal{E}_v \in \mathcal{E} \quad t_e(\mathcal{E}_u) <t_e(\mathcal{E}_v)\ \Leftrightarrow\ min_{s_u\in \mathcal{E}_u} t(s_u) < min_{s_v\in \mathcal{E}_v} t(s_v)$
  • Average cosine similarity
    $AvgSim(\mathcal{E}_u,\mathcal{E}_v) = {\sum_{s_u \in \mathcal{E}_u} \sum_{s_v \in \mathcal{E}_v} cos(s_u,s_v) \over \|\mathcal{E}_u\|\|\mathcal{E}_v\|}$

Dependencies를 결정하는 방법으로 5가지를 제시하고 있다.

• Complete-Link Modeling
  Assume that there are dependencies between all pairs of events.
  Direction of dependency is determined by the time-ordering
  $E' = \{(\mathcal{E}_u,\mathcal{E}_v)\ |\ t_e(\mathcal{E}_u) < t_e(\mathcal{E}_v)\}$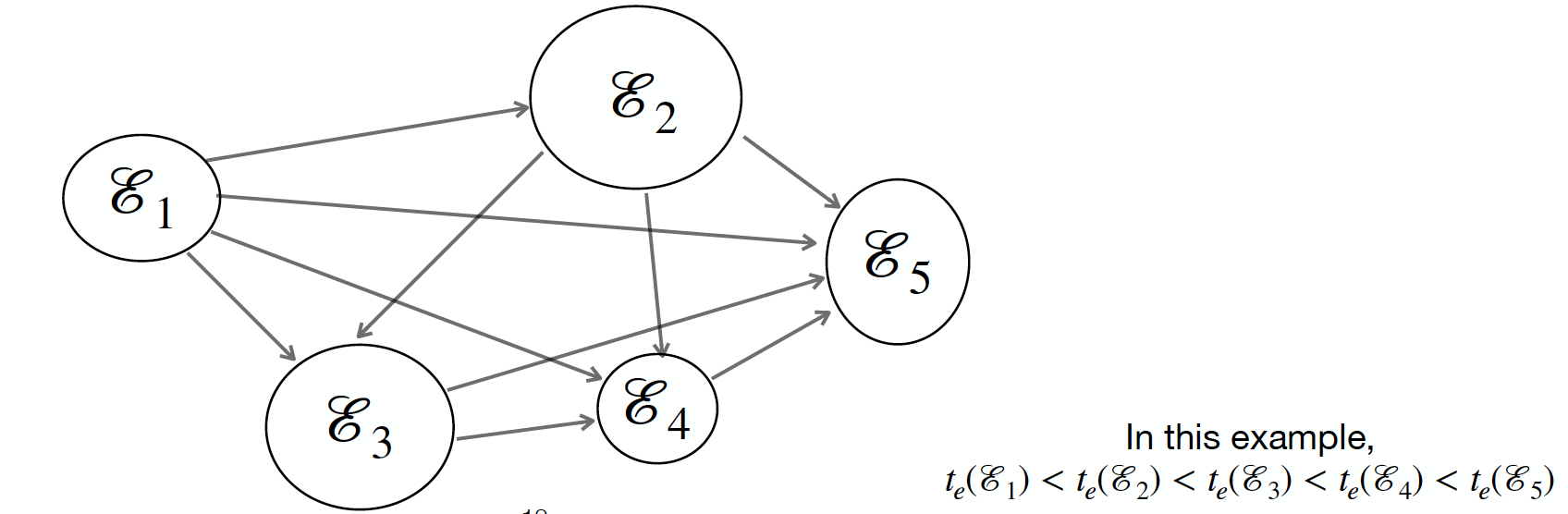

• Simple Thresholding
  An extension of the complete link model with an additional constraint
  $E' = \{(\mathcal{E}_u,\mathcal{E}_v)\ |\ AvgSim(\mathcal{E}_u,\mathcal{E}_v) > T\ \cap\ t_e(\mathcal{E}_u) < t_e(\mathcal{E}_v)\}$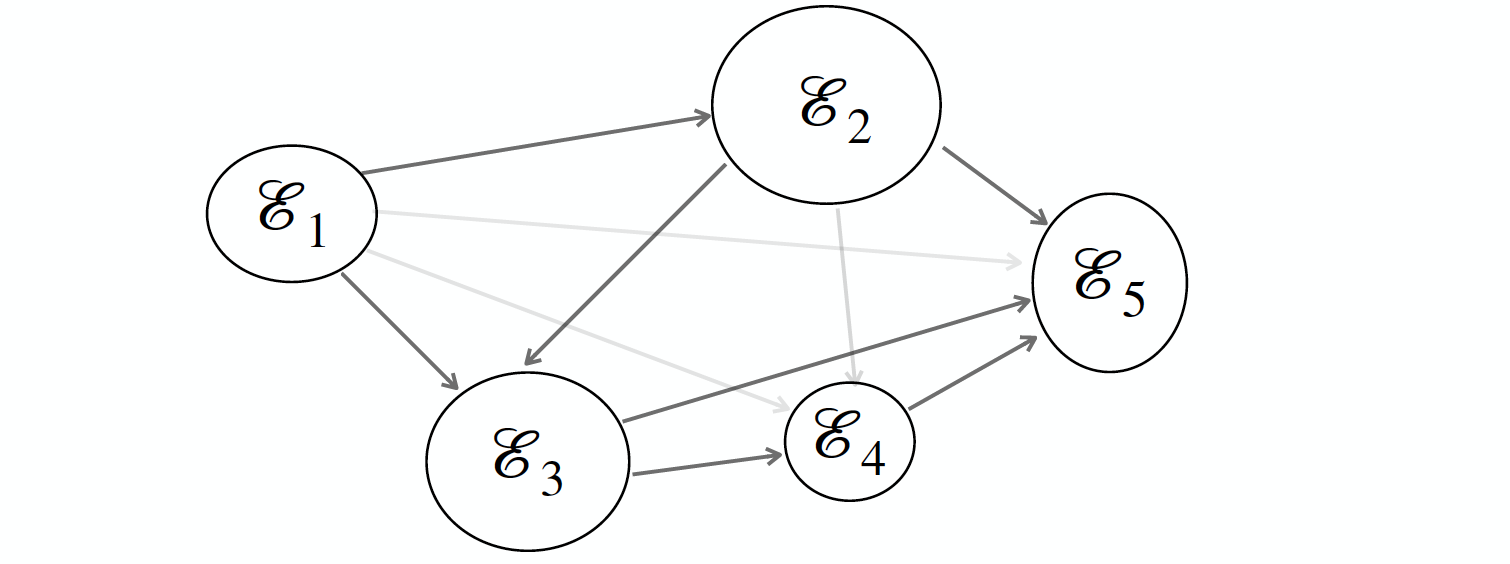

• Nearest Parent model
  Assume that each event can have at most one parent
  $E' = \{(\mathcal{E}_u,\mathcal{E}_v)\ |\ AvgSim(\mathcal{E}_u,\mathcal{E}_v) > T\ \cap\ t_e(\mathcal{E}_v) = t_e(\mathcal{E}_u) + 1\}$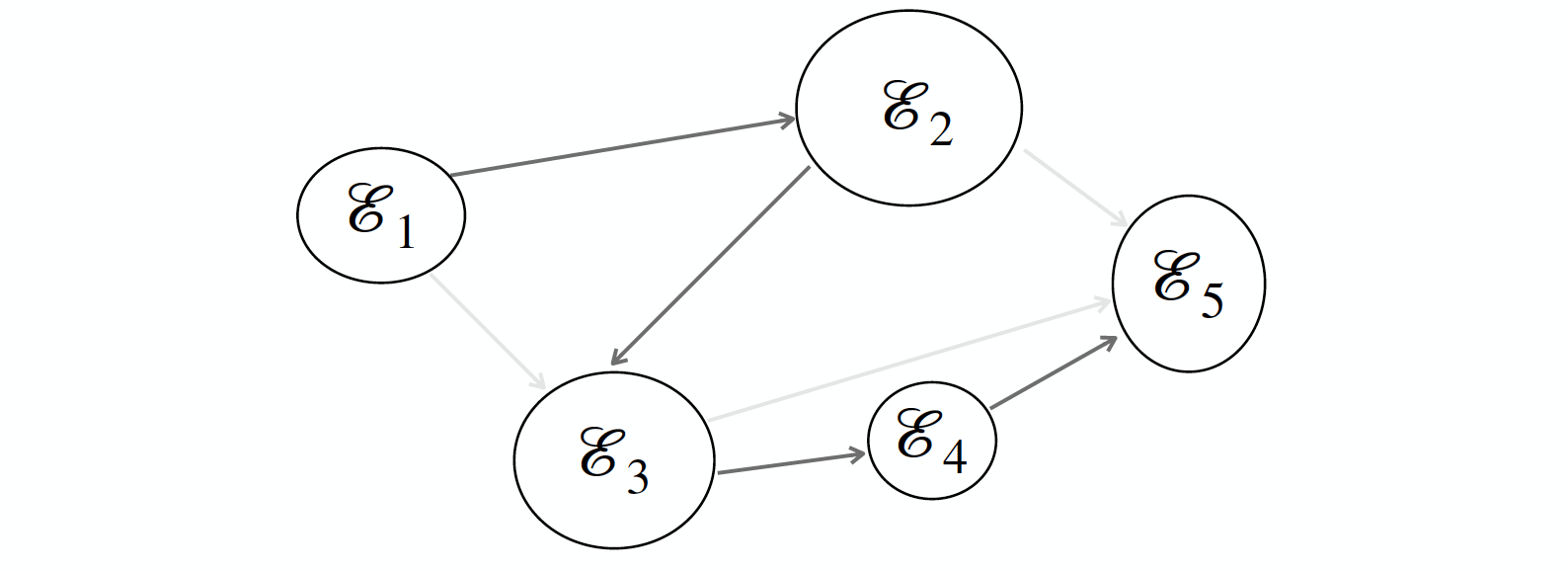

• Best Similarity Model
  Also assume that each event can have at most one parent
  $\mathcal{E}_v$is assigned a parent $\mathcal{E}_u$if only if $\mathcal{E}_u$is the most similar earlier event to $\mathcal{E}_v$
  $E' = \{(\mathcal{E}_u,\mathcal{E}_v)\ |\ AvgSim(\mathcal{E}_u,\mathcal{E}_v) > T\ \cap$
  $\mathcal{E}_u = argmax_{ \mathcal{E}_w:t_e(\mathcal{E}_w) < t_e(\mathcal{E}_v)}AvgSim(\mathcal{E}_w,\mathcal{E}_v)\}$

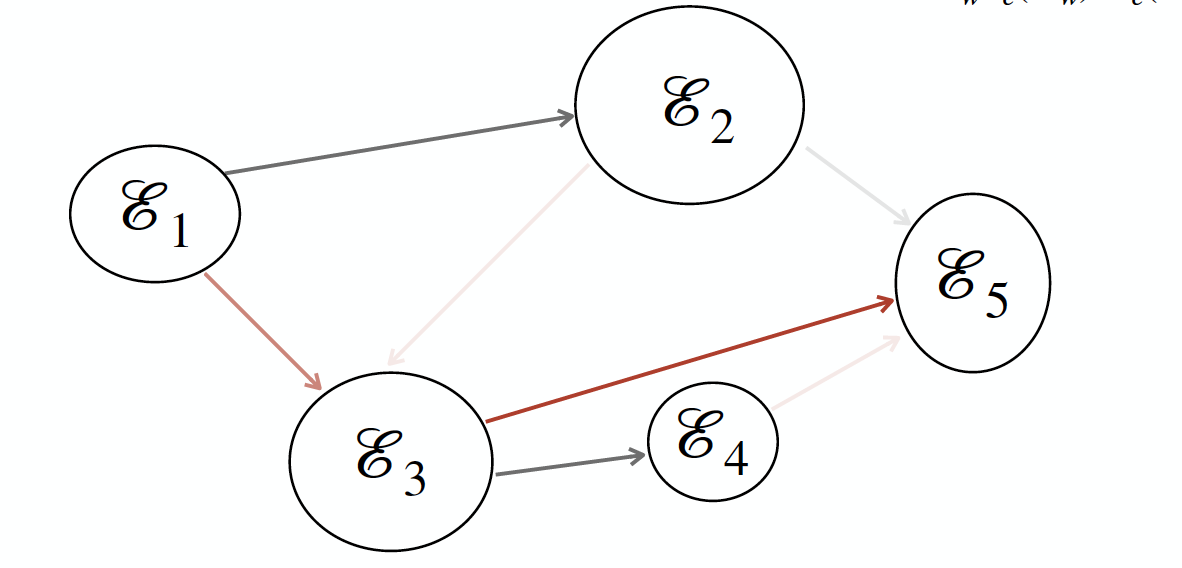
• Maximum Spanning Tree model
  Build maximum spanning tree using a greedy algorithm on the following
  fully connected weighted, undirected graph whose edges $\hat E$
  $\hat E = \{(\mathcal{E}_u,\mathcal{E}_v)\}\ \cap\ w(\mathcal{E}_u,\mathcal{E}_v) = AvgSim(\mathcal{E}_u,\mathcal{E}_v)$

Directed dependency edges $E$ are defined as follows. $E' = \{(\mathcal{E}_u,\mathcal{E}_v)\ |\ (\mathcal{E}_u,\mathcal{E}_v) \in MST(\hat E)\ \cap\ t_e(\mathcal{E}_u) < t_e(\mathcal{E}_v)\ $
$\cap\ AvgSim(\mathcal{E}_u,\mathcal{E}_v) > T\}$

• Combine Clustering and Dependencies
  In this paper, they tried several variation of the ACDT algorithm and tested each of dependencies.

As a result, $cos+TD+avg\text{-}lnk+Simple\ Thresholding$ outperforms.