정리중

Trains of Thought 정리

Connecting the dots의 User study에서 competitor로 나온 방법
정리 순서

• Event Threading in Connecting the dots
  • Brief definiton of Event Threading
  • How Event Threading Used in CTD
• Details of Event Threading
  • Notation
  • The difference between Event Threading and TDT
  • Problem Definition
  • Modeling(Clustering stories & Constructing Dependencies)

blah

Coverage

Goal

• Cover important aspect of the story

• Encourage diversity

• Coverage of a single document $cover_{d_i}(w):W \rightarrow [0,1]$
  document $d_i$가 feature $w$를 cover하는 양

Connectivity

number of lines of $Pi$ that intersect
$Conn(M) = \sum_{i<j}1(p_i \cap p_j \ne \emptyset )$

Objective Function : Trying it all together

3가지 특징( Coherence, Coverage, Connectivity )를 합쳐서 나타낸다.
BUT, Tradeoff 존재 ex) maximize Coherence → low-coverage chain maximize Connectivity → choose similar chain → low-coverage chain maximize Coverage → low-connectivity (no reason to re-use article)

Coherence 제약조건으로 사용, threshold $\tau$로 고정 coverage, connectivity를 어떻게 할것인가

if. primary objective = Connectivity,
문제점 : coherent line 이 group안에서 나타남. multiple similar lines을 동반(서로서로 intersect)
→ 이것들을 선택하면 connectivity는 상승하지만 map redundancy도 증가

그래서 primary objective = Coverage,
$\kappa$ : maximal coverage across maps with coherence $\geq \tau$

$\Rightarrow$ formulate problem
$PROBLEM2.2.\ Given\ a\ set\ of \ candidate\ documents\ D,$
$find\ a\ map\ M = (G,\Pi)\ over\ D\ which\ maximizes\ Conn(M)$
$s.t.\ Coherence(M) \geq \tau and\ Cover(M) = \kappa$

coverage maximize하고 connectivity maximize함. 문제 : 두 metro line이 d에서 intersect할때, coverage function이 set function이라서 d가 1번만 고려된다. 유사한 article d’으로 d를 교체할때, max-coverage-map은 자주 disconnected된다. → 문제를 완화시키기 위해 식 변형
$PROBLEM2.3.\ Given\ a\ set\ of \ candidate\ documents\ D,$
$find\ a\ map\ M = (G,\Pi)\ over\ D\ which\ maximizes\ Conn(M)$
$s.t.\ Coherence(M) \geq \tau \ and\ Cover(M) = (1-\epsilon)\kappa$

M의 크기 규정 : K lines of length at most l

Algorithm

접근과정 : graph로서 모든 coherent chain 나타내기 → 이 그래프를 사용하여 Coverage를 maximize하면서 K chain의 집합 찾기 → Coverage를 해치지 않으면서 Connectivity 증가시키기

Representing all coherent chains

모든 가능한 candidate찾는 것은 연산이 너무 많을 수 있음. → Divide and conquer사용 : 작은 chain으로 부터 긴 chain 만들기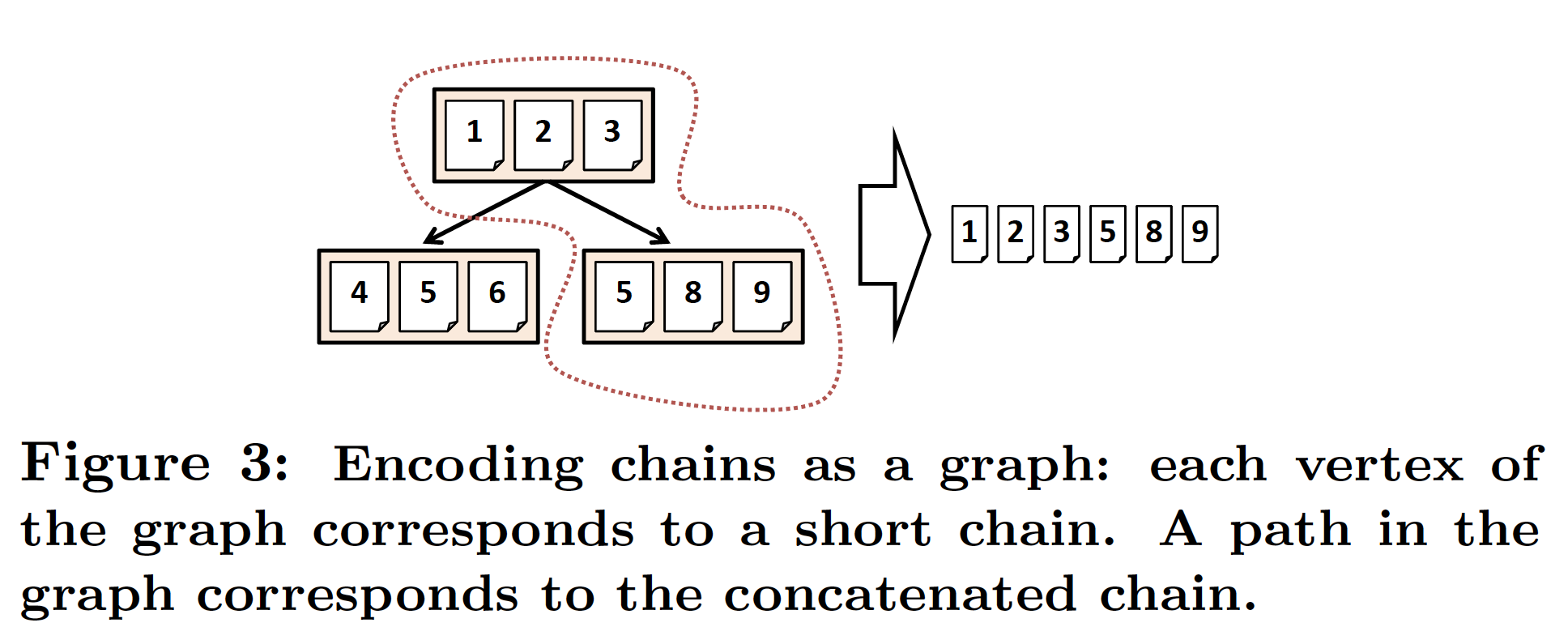

caution) comvine two strong chains may result in a much weaker chain.
point of discontinuity : $(d_1,...,d_k)$와 $(d_{k},...,d_{2k-1})$을 합칠때 두chain이 같은 storyline이라고 보장 못함.

$DEFINITION 3.1\ (m-COHERENCE).\ A\ chain(d_1,...,d_k)$ $has\ m \text{-}coherence\ \tau\ if\ each\ sub-chain\ of\ length\ m(d_{i},...d_{i+m-1}),$ $i=1,...k-m+1 \ has\ coherence\ at\ least\ \tau$

computation을 허용하는 highest m을 선택

2.3식 수정
$PROBLEM3.2.\ Given\ a\ set\ of \ candidate\ documents\ D,$
$find\ a\ map\ M = (G,\Pi)\ over\ D\ which\ maximizes\ Conn(M)$
$s.t.\ m \text{-}Coherence(M) \geq \tau \ and\ Cover(M) = (1-\epsilon)\kappa$

겹치는 값이 충분히 크면(m-1) 합치기

(obesrvation 3.3 생략.)

short coherent chain 찾기
general best-fit search strategy사용. sub-chain priority queue사용해서 highest coherence를 갖도록 길이 m까지 expand.